The Vertical Angle Theorem, or Proposition 15 in Euclid's Elements, is one of my favorites, because of its simplicity. You can produce two angles which are exactly equal in measure simply by drawing two intersecting straight lines. Even better, you draw two pairs of congruent angles whenever you simply draw two straight intersecting lines. Of course, "simply" is a bit of an understatement. You have to draw two perfectly straight, one-dimensional lines, but other than that, it's cake. (And I suppose those two lines should intersect in just one point. Or does that matter?) The angles in each pair that are congruent are called vertical angles.
The name has to do with the "vertex" sense of "vertical" instead of the "up and down" sense. Heath explains, by way of Proclus, the difference between vertical angles and adjacent angles (today, we would call these adjacent angles a linear pair). I've highlighted the part which clarifies the naming of vertical angles:
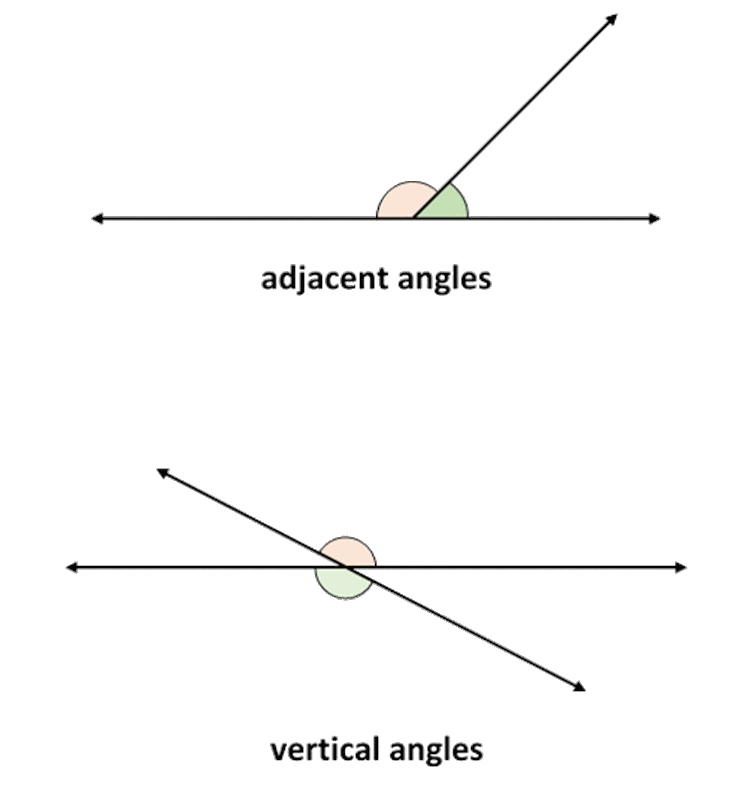The first term describes the angles made by two straight lines when one only is divided by the other, i.e., when one straight line meets another at a
point which is not either of its extremities, but is not itself produced beyond the point of meeting. When the first straight line is
produced, so that the lines cross at the point, they make two pairs of vertical angles (which are more clearly described as
vertically opposite angles), and which are so called because their convergence is from opposite directions to one point (the intersection of
the lines) as vertex.But the Proof Relies on "Adjacent Angles," a.k.a. Linear Pairs
The proof that vertical angles are congruent makes use of Proposition 13, which is a proof that the angles in a linear pair (the so-called adjacent angles) have measures that add up to \(\small\mathtt{180^\circ}\). Let's just assume that Proposition 13 is true for now and see how it is applied in Euclid's proof of the Vertical Angle Theorem.
For let the straight lines \(\small\mathtt{AB}\), \(\small\mathtt{CD}\) cut one another at the point \(\small\mathtt{E}\); I say that the angle
\(\small\mathtt{AEC}\) is equal to the angle \(\small\mathtt{DEB}\), and the angle \(\small\mathtt{CEB}\) to the angle \(\small\mathtt{AED}\).
For, since the straight line \(\small\mathtt{AE}\) stands on the straight line \(\small\mathtt{CD}\), making the angles \(\small\mathtt{CEA}\),
\(\small\mathtt{AED}\), the angles \(\small\mathtt{CEA}\), \(\small\mathtt{AED}\) are equal to two right angles. Again, since the straight line
\(\small\mathtt{DE}\) stands on the straight line \(\small\mathtt{AB}\), making the angles \(\small\mathtt{AED}\), \(\small\mathtt{DEB}\), the angles
\(\small\mathtt{AED}\), \(\small\mathtt{DEB}\) are equal to two right angles.The section highlighted shows two applications of Proposition 13, or what most would call the Linear Pair Postulate today. It just lets us say that those angles mentioned in the quotation are supplementary. It's interesting that Euclid uses "straight line" to describe both a ray and a line, and note that "two right angles" is used instead of what we would substitute with "a straight angle." This has to do with Euclid's definition of angle (Definition 1.8): "A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line."
But the angles \(\small\mathtt{CEA}\), \(\small\mathtt{AED}\) were also proved equal to two right angles; therefore the angles \(\small\mathtt{CEA}\),
\(\small\mathtt{AED}\) are equal to the angles \(\small\mathtt{AED}\), \(\small\mathtt{DEB}\).Let the angle \(\small\mathtt{AED}\) be subtracted from each; therefore the remaining angle \(\small\mathtt{CEA}\) is equal to the remaining angle \(\small\mathtt{BED}\). Similarly it can be proved that the angles \(\small\mathtt{CEB}\), \(\small\mathtt{DEA}\) are also equal. Therefore etc.
Once we get that \(\measuredangle\small\mathtt{CEA}\) + \(\measuredangle\small\mathtt{AED}\) = \(\measuredangle\small\mathtt{AED}\) + \(\measuredangle\small\mathtt{DEB}\), then we subtract \(\measuredangle\small\mathtt{AED}\) from both sides of the equation to see that the remaining angles are congruent. Rinse and repeat from the beginning for the other pair of vertical angles.
Assumptions and Questions
We see in the last part of the proof the use of Postulate 4 ("That all right angles are equal to one another"), Common Notion 1 ("Things which are equal to the same thing are also equal to one another"), and Common Notion 3 ("If equals be subtracted from equals, the remainders are equal"). What's missing is some assurance that no matter how I draw the two straight lines that intersect at a point, I can still do this proof.