The Side-Angle-Side Axiom Maybe?

The following quotation is from Euclid's Elements. It's what we would call a statement of the Side-Angle-Side Congruence Theorem (SAS), but in Elements it is Proposition I.4. Not exactly a model of precision here:

If two triangles have the two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, they will also have the base equal to the base, the triangle will be equal to the triangle, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend.

The "proof" that Euclid offers for SAS relies completely on his Common Notion 4, which says that "things which coincide with one another are equal to one another"--an assertion that he accepts without proof. Some refer to this method of proof as "proof by superposition." Let's run through Euclid's (translated) words to see how he does it. I'll highlight every spot where Common Notion 4 is applied (or is thought to be applied).

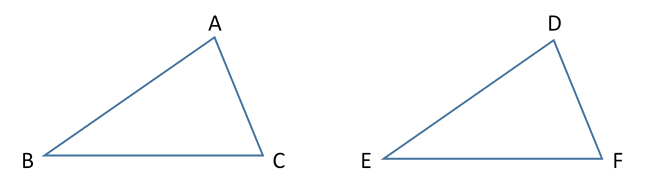
Let \(\small\mathtt{ABC, DEF}\) be two triangles having the two sides \(\small\mathtt{AB, AC}\) equal to the two sides \(\small \mathtt{DE, DF}\) respectively, namely \(\small\mathtt{AB}\) to \(\small\mathtt{DE}\) and \(\small\mathtt{AC}\) to \(\small\mathtt{DF}\), and the angle \(\small\mathtt{BAC}\) equal to the angle \(\small\mathtt{EDF}\). . . .


If the triangle \(\small\mathtt{ABC}\) be applied to the triangle \(\small\mathtt{DEF}\), and if the point \(\small\mathtt{A}\) be placed on the point \(\small\mathtt{D}\) and the straight line \(\small\mathtt{AB}\) on \(\small\mathtt{DE}\), then the point \(\small\mathtt{B}\) will also coincide with \(\small\mathtt{E}\), because \(\small\mathtt{AB}\) is equal to \(\small\mathtt{DE}\).

It's pretty amazing--and, depending on who you talk to, wonderful or sad--how little geometry has changed since the veritable father of the subject started writing it down over 2000 years ago. But anyway, here we see the typical "Given"s followed by what amounts to an astounding assertion: that if we place \(\small\mathtt{\overline{AB}}\) on top of \(\small\mathtt{\overline{DE}}\) such that point \(\small\mathtt{A}\) lines up with point \(\small \mathtt{D}\), then point \(\small\mathtt{B}\) will line up with point \(\small\mathtt{E}\) because \(\small\mathtt{\overline{AB} \cong \overline {DE}}\).

The reason this assertion is astounding is that it's actually the converse of Common Notion 4. While the idea that "things which coincide with one another are equal to one another" is unobjectionable, at least in plane geometry, the converse--that things which are equal to one another coincide with one another--is insanity. Two equal things could be in different places.

Again, \(\small\mathtt{AB}\) coinciding with \(\small\mathtt{DE}\), the straight line \(\small\mathtt{AC}\) will also coincide with \(\small\mathtt {DF}\), because the angle \(\small\mathtt{BAC}\) is equal to the angle \(\small\mathtt{EDF}\); hence the point \(\small\mathtt{C}\) will also coincide with the point \(\small\mathtt{F}\), because \(\small\mathtt{AC}\) is again equal to \(\small\mathtt{DF}\). But \(\small \mathtt{B}\) also coincided with \(\small\mathtt{E}\); hence the base \(\small\mathtt{BC}\) will coincide with the base \(\small\mathtt {EF}\).

Thus the whole triangle \(\small\mathtt{ABC}\) will coincide with the whole triangle \(\small\mathtt{DEF}\) and will be equal to it. And the remaining angles will also coincide with the remaining angles and will be equal to them, the angle \(\small\mathtt{ABC}\) to the angle \(\small\mathtt{DEF}\), and the angle \(\small\mathtt{ACB}\) to the angle \(\small\mathtt{DFE}\).

Only the last of those highlighted statements seems justified, but it is of course built on top of all the wobbly ones that came before it.


Axiomatizations

To wrap this up, let's take a look at some helpful notes on this "theorem," written by Sir Thomas Heath, whose translation I've been quoting in this article. I think it's amazing to watch both Heath and the person he quotes, Peletier, fanboyishly defend Euclid.

Euclid obviously used the method of superposition with reluctance. . . . Mr Bertrand Russell observes that Euclid would have done better to assume I.4 as an axiom, as is practically done by Hilbert. It may be that Euclid himself was as well aware of the objections to the method as are his modern critics; but at all events those objections were stated, with almost equal clearness, as early as the middle of the 16th century.

Peletarius (Jacques Peletier) has a long note on this proposition in which he observes that, if superposition of lines and figures could be assumed as a method of proof, the whole of geometry would be full of such proofs. . . . The theorem, he adds, is obvious in itself and does not require proof; although it is introduced as a theorem, it would seem that Euclid intended it rather as a definition than a theorem, "for I cannot think that two angles are equal unless I have a conception of what equality of angles is."

Hilbert did indeed make SAS an axiom.