So, Pick's Theorem involves some interesting terminology, like lattice polygon, that you don't hear in your typical geometry class. And it can involve a neat methodology, mathematical induction, which isn't talked about enough, if at all, in high school--and which I won't talk about in this installment.
At the moment, you can click and drag on the dot grid above to draw stuff and see the boundary points of your polygons circled, and in the future, I'll hook this up with some more magic to highlight what Pick's theorem talks about. Play with it to see what makes it tick.
So, what does this theorem say? It says that when you draw any lattice polygon, you can count the points on the interior, add that to half the number of points that lie on the sides (including the vertices), and subtract 1, and that will give you the area value of the polygon.

As that definition at the link above will tell you, a lattice polygon is a polygon whose vertices are all on the points of a lattice, which is a "regularly spaced array of points." The figure at the right shows a trapezoid I drew on my homemade lattice above. Pick's Theorem says that the area of the trapezoid is equal to \(\small\mathtt{I_{p} + \frac{1}{2}B_{p} - 1}\). That is, the number of interior points, \(\small\mathtt{I_{p}}\), plus half the number of boundary points (including the vertices), \(\small\mathtt{B_{p}}\), minus 1 is equal to the area.
Compare the result of this formula to what you get when you find the area of the trapezoid using base and height measures: \(\small\mathtt{A = \frac{1}{2}h \cdot (b_{1} + b_{2})}\). And of course, draw your own to see. Think ridiculously simple, like a unit square, for example. Or ridiculously complex. Try to break the formula.
Always Start Simple
As far as proving stuff, do what mathematicians do--instead of trying to tackle a really abstract and complex problem all at once, start with simpler instances of the general case and don't tell anyone until you've solved the harder problem. So, instead of "any lattice polygon," start with "any lattice rectangle."

How many interior points are there in any lattice rectangle? Well, if you draw a rectangle on the lattice above, you will see that the interior points of a lattice rectangle form a smaller rectangle of their own. If the height of the original rectangle is \(\small\mathtt{h}\) units, then the smaller rectangle will have \(\small\mathtt{h - 1}\) points on its height. The same goes for the width, so the number of points on the interior of the rectangle will be \(\small\mathtt{(h - 1)(w - 1)}\). (You just have to get used to going back and forth between "units" and "points" in this explanation for it to make the most sense.)
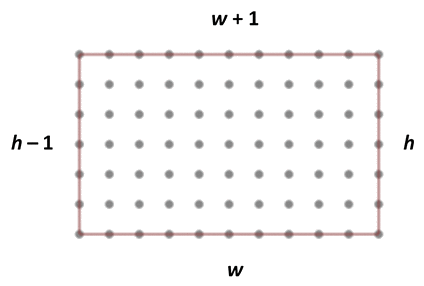
What about boundary points? We can traverse the boundary of a rectangle, again relating the number of points we count to the width and height. So, going clockwise from the top of the rectangle at the left, first I count \(\small\mathtt{w + 1}\) points on the width (its width is 10 units, but there are 11 points). Then I count \(\small\mathtt{h}\) points along the right side (the height of the rectangle is 6 units, and this is the number I count, because I have already counted the top right vertex point). And so on. Adding up all the points and simplifying, we get \(\small\mathtt{2w + 2h}\) for the number of boundary points of a lattice rectangle.
Finally, Pick's theorem says that \[\mathtt{A = \frac{2w + 2h}{2} + (h - 1)(w - 1) - 1}\] And this simplifies to \(\small\mathtt{hw}\), the area of the rectangle--and, more generally, any rectangle.
Let's remember to talk more about this whole theorem at some point in the future. In the meantime, here's a great paper on Pick's Theorem with some nice explanations.
Postscript
To my point above about mathematicians' silence on interim results and process, I came across this wonderful quotation by mathematician Alexander Grothendieck, who passed away in November of 2014. Here he talks about 'speculation' in mathematics (in a 1983 letter):