The Inscribed Angle Theorem

Check out the demo above and fiddle with the sliders for just a minute to see how they affect the diagram. The "a" and "b" sliders control the sides of the central angle (the angle with red sides)--and increase and decrease its measure. The value O on Line 8 shows the measure of the central angle. The "c" slider controls the vertex of the inscribed angle (the angle with the dashed sides), and the "r" slider increases and decreases the size of the circle.

The idea here is to get close to demonstrating the inscribed angle theorem, which says that the measure of the inscribed angle (dashed sides) is always half the measure of the central angle (red sides). It seems that this is true for most of the positions you can get to above, but it certainly doesn't seem true for every position (like when \(\small \mathtt{a = 0, b = -2.2, c = -1}\)).

The Sorta Kinda Proof

The way that this is typically done is to look at 3 different cases (shown below)--one where the center of the circle is inside the inscribed angle; one where it's outside the angle, and one where the center lies on one of the sides of the inscribed angle. Notice that we get to use the Greek letters alpha (\(\small\mathtt{\alpha}\)) and beta (\(\small\mathtt{\beta}\)) in order to make this seem really cool and sophisticated.

Inside the Angle	Outside the Angle	On the Line
First, construct a diameter that runs through the vertex of the inscribed angle (and of course the center). In this case, the green dashed line segment, \(\overline{\small\mathtt {BQ}}\), is our diameter. This makes \(\overline{\small\mathtt{OB}}\) a radius, so \(\overline{\small\mathtt{OB}} \cong \overline{\small\mathtt{OR}} \cong \overline{\small\mathtt{OS}}\). The base angle theorem tells us that if two sides of a triangle are congruent, then the angles opposite those sides are also congruent. The congruent radii give us 2 pairs of congruent angles, as you can see below: \(\small\measuredangle\mathtt{OBR} \cong \small\measuredangle\mathtt{ORB}\), and \(\small\measuredangle\mathtt{OBS} \cong \small\measuredangle\mathtt{OSB}\). It's tempting for me to think, by the way, that all of the shaded angles above are congruent, because they are all opposite the radiuses, which are all congruent. But that's not true! Anyway, although I deleted the \(\small\mathtt{\alpha}\) and \(\small\mathtt{\beta}\) above to make the diagram cleaner, I hope you can see that the measure of the inscribed angle, \(\small\measuredangle\mathtt{B}\), is 1 pink + 1 green. Now we have to show that the measure of the central angle is twice that, or 2 × (pink + green), or 2(pink) + 2(green). And so it is! Because of the exterior angle theorem, we know that the measure of \(\small\measuredangle\mathtt{SOQ}\) is equal to pink + pink and the measure of \(\small\measuredangle\mathtt{ROQ}\) is equal to green + green. This means that the central angle, \(\small\measuredangle\mathtt{SOR}\), has a measure that is twice the measure of the inscribed angle, \(\small\measuredangle\mathtt{SBR}\).	Diameter \(\overline{\small\mathtt{OB}}\) again reveals some congruent radii, marked with red tick marks. The base angle theorem also reveals some congruent angles--marked again in pink and green. 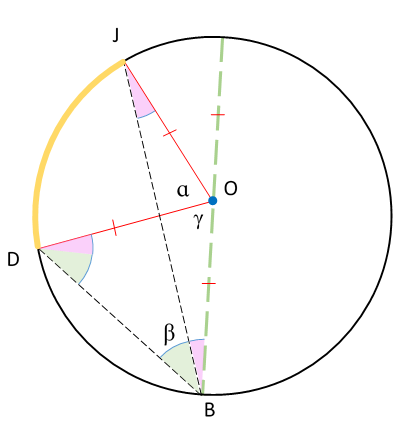Once we've got this puppy thoroughly marked up, we don't need to do anything else except remember that the sum of the measures of the interior angles of a triangle is \(\small \mathtt{180^\circ}\). But, let's label some vertices to make this easier to talk about: Notice that \(\small\mathtt{\beta}\) = green. And, just for convenience, we make use of the Greek letter gamma (\(\small\mathtt{\gamma}\)). For \(\small\Delta\mathtt{JOB}\), 2(pink) + \(\small\mathtt{\alpha}\) + \(\small\mathtt{\gamma}\) = \(\small\mathtt{180^\circ}\). For \(\small\Delta\mathtt{BOD}\), 2(pink) + 2\(\small\mathtt{\beta}\) + \(\small\mathtt{\gamma}\) = \(\small\mathtt{180^\circ}\). The only difference between those equations is that one uses \(\small\mathtt{\alpha}\) and the other uses 2\(\small\mathtt{\beta}\). This means that 2\(\small\mathtt{\beta}\) = \(\small\mathtt{\alpha}\), or 2 times the measure of the inscribed angle is equal to the measure of the central angle.	This case is the most straightforward--at least as I've drawn it here. The base angle theorem once again allows us to mark congruent angles. The angles marked \(\small\mathtt{\alpha}\) and \(\small\mathtt{\gamma}\) together form a linear pair, which means they "add up to a line." In more mathy speak, those two angle measures together have a sum of \(\small\mathtt{180^\circ}\). So, we get \(\small\mathtt{\alpha} + \small\mathtt{\gamma} = \small\mathtt{180^\circ}\) and also, looking at the triangle, we see that 2\(\small\mathtt{\beta} + \small\mathtt {\gamma} = \small\mathtt{180^\circ}\). Thus, 2\(\small\mathtt{\beta} = \small\mathtt{\alpha}\), or the measure of the central angle is twice that of the measure of the inscribed angle.

The Remaining Problem

When you played with the inscribed angle on the Desmos graph above, you saw that there were situations when the inscribed angle was definitely not half the measure of the central angle. This was when the inscribed angle was "facing toward" the central angle, as you can see at the right.

You can see some of the more technical language for this exception at this link, where, incidentally, the theorem is called the central angle theorem.