The name of this special little curve--the diamond-shaped one that is partly in dashed lines at the right--is the cissoid and is pronounced SISS-oid. Specifically, this cissoid at the right is sometimes called the Cissoid of Diocles. The Greek word that is the ancestor to "cissoid" apparently means "ivy-shaped," and it is a little disappointing to me that I couldn't find a connection to "kiss," seeing as the cissoid (in all quadrants of the circle) resembles the shape of the mouth opening when cartoonish lips are puckered cartoonishly.
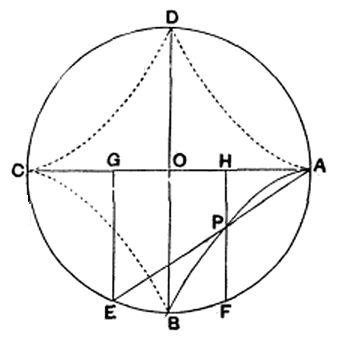
The following appears in Heath's translation of the Elements as a method for generating the cissoid:
Draw \(\overline{\small\mathtt{EG}}\), \(\overline{\small\mathtt{FH}}\) perpendicular to \(\overline{\small\mathtt{CA}}\). Join \(\small\mathtt{AE}\) and let \(\small\mathtt{P}\) be its intersection with \(\overline{\small\mathtt{FH}}\).
The cissoid is the locus of all the points \(\small\mathtt{P}\) corresponding to different positions of \(\small\mathtt{E}\) on the quadrant \(\small\mathtt{BC}\) and of \(\small\mathtt{F}\) at an equal distance from \(\small\mathtt{B}\) along the arc \(\small\mathtt{BA}\).
Let's Do It Ourselves
Play with the diagram at the right to see how the construction above works. Drag the blue point (this is point \(\small\mathtt{E}\) in the diagram above) in Quadrant III to move the orange intersection point (\(\small\mathtt{P}\) above) to generate the cissoid. In this version, I've also included the various reflections of point \(\small\mathtt{P}\) in the different quadrants. Press Reset to clear the circle.
I don't know about you, but I certainly see puckering. I'm also reminded of theater curtains when I look at the curves in Quadrants I and II. Is there anything "cissoidal" about the contraptions they use to open these curtains? Or maybe there's something similar in the way our kissing muscles do their jobs.
The Equation Is In the Code
For the little cissoid-making machine above, here is the code that assigns the \(\small\mathtt{y}\)-value of point \(\small\mathtt{P}\):

Hopefully it's straightforward to see that this is a point-slope equation just moved around a little. I use H.x, the \(\small\mathtt{x}\)-value of point \(\small\mathtt{H}\), instead of the one for point \(\small\mathtt{P}\) because they are the same. The cool thing is that when we translate this into Cartesian coordinates using the coordinates of the circle as a reference (and shifting the circle to center at the origin), we get this loveliness: \[\small\mathtt{y = (\frac{\sqrt{r^2 - x^2}}{x - r} \cdot -2x) + \sqrt{r^2 - x^2}}\]
This is not quite the equation for the cissoid we're looking at, but it is one piece. We can put all the pieces together like in the Desmos graph below. Our equation above is the first equation listed for the graph. You should see that the curves inside the circle don't tell the whole story: