The structure of this proof comes from a neat little book called Geometry Revisited. But I'll start with something the authors of that book ask us to recall: "that the areas of triangles with equal altitudes are proportional to the bases of the triangles."
The equation below the left triangle shown is of the form \(\small\mathtt{A_1 = b_1 \cdot k}\) and the equation for the triangle to the right is \(\small\mathtt{A_2 = b_2 \cdot k}\), where \(\small\mathtt{A}\) stands for area (in square pixels) and \(\small\mathtt{b}\) stands for base length (in pixels). Because the two triangles have equal heights (equal altitudes; in this case 180 pixels), we can use the constant \(\small\mathtt{k}\) to represent \(\small\mathtt{\frac{1}{2} \cdot h}\) in each area equation.
You can drag the bottom left vertex of the leftmost triangle or the bottom right vertex of the rightmost triangle to change the base length of either triangle. Note that the ratio of the areas is equal to the ratio of the base lengths (i.e., "the areas of triangles with equal altitudes are proportional to the bases of the triangles"). Since we have \(\small\mathtt{A_1 = b_1 \cdot k}\) and \(\small\mathtt{A_2 = b_2 \cdot k}\), then \(\small\mathtt{\frac{A_1}{b_1}}\) gives us the same number as \(\small\mathtt{\frac{A_2}{b_2}}\), namely \(\small\mathtt {k}\).
What the Theorem Says and a Proof
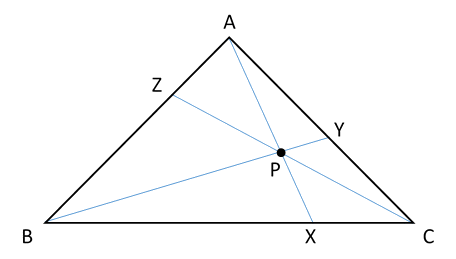
Draw three line segments \(\overline{\small\mathtt{AX}}\), \(\overline{\small\mathtt{BY}}\), and \(\overline{\small\mathtt{CZ}}\) inside a triangle, each from a vertex to the opposite side. Ceva's Theorem (Ceva is pronounced CHEH-vuh) says that if the line segments meet at a point (are concurrent), then \(\small\mathtt{\frac{BX}{XC} \cdot \frac{CY}{YA} \cdot \frac{AZ}{ZB}}\) = 1.
So, let's see. Given what we learned above, \(\small\mathtt{\frac{BX}{XC}}\) = \(\mathtt{\frac{A_{ABX}}{A_{AXC}}}\). Each of these ratios is also equal to \(\mathtt{\frac{A_ {PBX}}{A_{PXC}}}\).
That last ratio is also equal to \(\mathtt{\frac{A_{ABX} - A_{PBX}}{A_{AXC} - A_{PXC}}}\), because we can safely subtract across the numerators and then the denominators when working with equal part-to-part ratios (can you work out why?). Finally, subtracting the area of \(\small\Delta\)\(\small\mathtt{PBX}\) from the area of \(\small\Delta\)\(\small \mathtt{ABX}\) gives us the area of \(\small\Delta\)\(\small\mathtt{ABP}\), or \(\small\mathtt{A_{ABP}}\). Similarly, subtracting the area of \(\small\Delta\)\(\small\mathtt{PXC}\) from the area of \(\small\Delta\)\(\small\mathtt{AXC}\) gives us the area of \(\small\Delta\)\(\small\mathtt{CAP}\), or \(\small\mathtt{A_{CAP}}\). We have wound up with a chain of equals signs, giving us, in the end, \(\small\mathtt{\frac{BX}{XC}}\) = \(\small\mathtt{\frac{A_{ABP}}{A_{CAP}}}\).
So now we do that with the other two sides. Here are all three equals-sign chains:

- \(\small\mathtt{\frac{BX}{XC}}\) = \(\mathtt{\frac{A_{ABX}}{A_{AXC}}}\) = \(\mathtt{\frac{A_{PBX}}{A_{PXC}}}\) = \(\mathtt{\frac{A_{ABX} - A_{PBX}}{A_ {AXC} - A_{PXC}}}\) = \(\mathtt{\frac{A_{ABP}}{A_{CAP}}}\)
- \(\small\mathtt{\frac{CY}{YA}}\) = \(\mathtt{\frac{A_{BCY}}{A_{BYA}}}\) = \(\mathtt{\frac{A_{PCY}}{A_{PYA}}}\) = \(\mathtt{\frac{A_{BCY} - A_{PCY}}{A_{BYA} - A_ {PYA}}}\) = \(\mathtt{\frac{A_{BCP}}{A_{ABP}}}\)
- \(\small\mathtt{\frac{AZ}{ZB}}\) = \(\mathtt{\frac{A_{CAZ}}{A_{CZB}}}\) = \(\mathtt{\frac{A_{PAZ}}{A_{PZB}}}\) = \(\mathtt{\frac{A_{CAZ} - A_{PAZ}}{A_{CZB} - A_ {PZB}}}\) = \(\mathtt{\frac{A_{CAP}}{A_{BCP}}}\)
Then just cross out stuff to see that \(\mathtt{\frac{A_{ABP}}{A_{CAP}} \cdot \frac{A_{BCP}}{A_{ABP}} \cdot \frac{A_{CAP}}{A_{BCP}}}\) = 1, which means that \(\small\mathtt {\frac{BX}{XC} \cdot \frac{CY}{YA} \cdot \frac{AZ}{ZB}}\) = 1.
Huzzah!